如图,在矩形ABCD中,点E、F分别在边AD、DC上,△ABE∽△DEF,AB=6,AE=9,DE=2,则EF的长为(保留三位有效数字).
题目答案
您的答案
答案解析
分析:
已知△ABE∽△DEF,那么点A、D对应,点B、E对应,点E、F对应,首先根据相似三角形得到的比例线段求出DF的长,再由勾股定理求得EF的值.
解答:
解:∵四边形ABCD是矩形,
∴∠A=∠D=90°;
∵△ABE∽△DEF,
∴$\frac {AB}{AE}$=$\frac {DE}{DF}$,即$\frac {6}{9}$=$\frac {2}{DF}$,解得DF=3;
在Rt△DEF中,DE=2,DF=3,由勾股定理得:
EF=$\sqrt {}$=$\sqrt {13}$≈3.61.
故答案为:3.61.
点评:
此题主要考查的是相似三角形的性质,找准对应顶点是解题的关键.
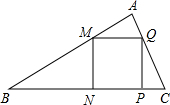 已知正方形MNPQ内接于△ABC(如图所示),若正方形边长是3,BC=12,则△ABC的面积=
已知正方形MNPQ内接于△ABC(如图所示),若正方形边长是3,BC=12,则△ABC的面积=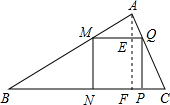 作AE⊥BC于F,交MQ于E.
作AE⊥BC于F,交MQ于E.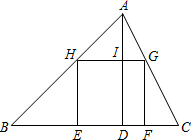
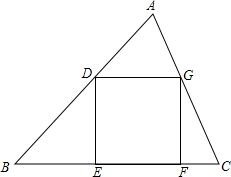
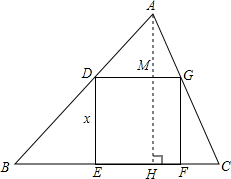 解:过点A作AH⊥BC于点H,交DG于点M,
解:过点A作AH⊥BC于点H,交DG于点M,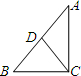 解:∵Rt△ABC中,CD是斜边AB上的中线,CD=4,
解:∵Rt△ABC中,CD是斜边AB上的中线,CD=4,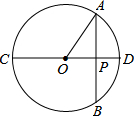
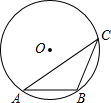
 解:连接AO并延长到圆上一点D,连接BD,
解:连接AO并延长到圆上一点D,连接BD,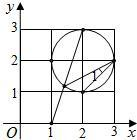
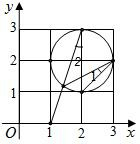

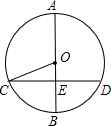
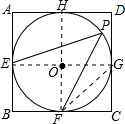 解:连接HF,EG,FG,
解:连接HF,EG,FG,