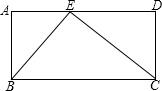
如图所示,等腰梯形ABCD中,DC∥AB,对角线AC与BD交于点O,AD=DC,AC=BD=AB.若∠ABD=α,则α=°.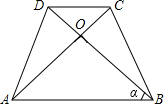
题目答案
您的答案
答案解析
分析:
根据DC∥AB,AD=DC,可以得到∠DAC=∠BAC,又等腰梯形ABCD中∠BAC=∠ABD,在等腰△ABD中,BD=AB利用三角形内角和定理列式求解即可.
解答:
解:∵DC∥AB,
∴∠DCA=∠CAB,
∵AD=DC,
∴∠DCA=∠DAC,
∴∠DAC=∠CAB,
∴∠DAB=2∠CAB=2α,
在等腰梯形ABCD中,∠CAB=∠ABD=α,
又∵BD=AB,
∴∠DAB=∠ADB,
∴在△ABD中,
α+2×2α=180°,
解得α=36°.
点评:
考查等腰梯形的性质,利用等边对等角的性质推出角的关系再利用三角形内角和定理求出角是解题的关键.
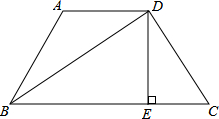
 解:如图:过点C作CD⊥EF,
解:如图:过点C作CD⊥EF,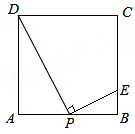
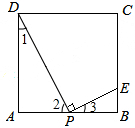 解:设AP=x,BE=y.
解:设AP=x,BE=y.
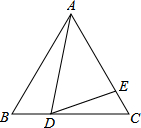


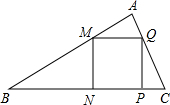 已知正方形MNPQ内接于△ABC(如图所示),若正方形边长是3,BC=12,则△ABC的面积=
已知正方形MNPQ内接于△ABC(如图所示),若正方形边长是3,BC=12,则△ABC的面积=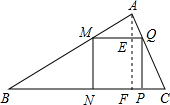 作AE⊥BC于F,交MQ于E.
作AE⊥BC于F,交MQ于E.