如图,△ABC和△DCE都是边长为4的等边三角形,点B、C、E在同一条直线上,连接BD,则BD的长为( )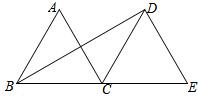
题目答案
您的答案
答案解析
分析:
根据等边三角形的性质、等腰三角形的性质和三角形的外角的性质可以发现∠BDE=90°,再进一步根据勾股定理进行求解.
解答:
解:∵△ABC和△DCE都是边长为4的等边三角形,
∴∠DCE=∠CDE=60°,BC=CD=4.
∴∠BDC=∠CBD=30°.
∴∠BDE=90°.
∴BD=$\sqrt {}$=4$\sqrt {3}$.
故选D.
点评:
此题综合应用了等边三角形的性质、等腰三角形的性质、三角形的外角的性质和勾股定理.

 ×3x×4x=6x_=54.
×3x×4x=6x_=54.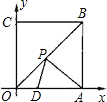
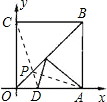 解:连接CD,交OB于P.则CD就是PD+PA和的最小值.
解:连接CD,交OB于P.则CD就是PD+PA和的最小值.