等腰直角三角形的三边之比为（ ）
分析：
先设等腰直角三角形的一个直角边长为a，根据勾股定理计算出其斜边的长，然后三边相比即可．
解答：
解：设等腰直角三角形的一个直角边长为a，
则另一边长也为a，其斜边长为$\sqrt {}$=$\sqrt {2}$a，
所以等腰直角三角形的三边之比为a：a：$\sqrt {2}$a=1：1：$\sqrt {2}$．
故选B．
点评：
本题考查学生对等腰直角三角形和勾股定理的理解和掌握，解得此题的关键是利用勾股定理求出其斜边的长，此题难度不大，是一道基础题．
如果一个三角形的三边之比为1：$\sqrt {2}$：1，那么最小边所对的角为（ ）
分析：
根据勾股定理的逆定理进行解答即可．
解答：
解：设三角形的三边分别为x、$\sqrt {2}$x、x，
∴x+x_=($\sqrt {2}$x)_，
∴此三角形为直角三角形，
∴最大角为90°，
∵三边的比为1：$\sqrt {2}$：1，
∴此三角形为等腰直角三角形，
∴最小角为45°．
故选B．
点评：
本题考查的是等腰直角三角形的知识及勾股定理的逆定理，即若一个三角形的三边满足a_+b_=c_，则这个三角形是直角三角形．
一个等腰直角三角形的斜边为 4$\sqrt {2}$，则其面积为（ ）
分析：
设等腰直角三角形的两直角边为x，由勾股定理得出方程x+x_=(4$\sqrt {2}$)_，求出x，再根据三角形的面积公式求出即可．
解答：
解：设等腰直角三角形的两直角边为x，
则由勾股定理得：x+x_=(4$\sqrt {2}$)_，
解得：x=4，
即等腰直角三角形的面积是：$\frac {1}{2}$×4×4=8，
故选B．
点评：
本题考查了等腰直角三角形性质、勾股定理、三角形的面积等知识点，关键是求出等腰直角三角形的直角边，用了方程思想．
如果一个等腰直角三角形的面积为2，则斜边长为（ ）
分析：
先设等腰直角三角形一个直角边为x，利用等腰直角三角形的面积为2，求出等腰直角三角形一个直角边，再用勾股定理即可求出其斜边的长．
解答：
解：设等腰直角三角形一个直角边为x，
则x×x×$\frac {1}{2}$=2，解得x=2，
由勾股定理得斜边长为2$\sqrt {2}$．
故选C．
点评：
此题考查学生对等腰直角三角形和勾股定理的理解和掌握，解答此题的关键是先求出等腰直角三角形一个直角边的长，这是此题的突破点，难度不大，是一道基础题．
如图，△ABC中，∠ACB=90°，∠A=45°，AC=6，则AB边上的高CD为( )．
分析：
由已知直角三角形ABC中，∠ACB=90°，∠A=45°，CD是AB边上的高可结合等腰直角三角形的性质得到CD的值．
解答：
解：∵∠ACB=90°，∠A=45°，
∴∠B=45°，
∴AC=BC，
∵AC=6，
∴AB=$\sqrt {2}$AC=6$\sqrt {2}$，
又∵CD⊥AB，
∴AD=BD=$\frac {1}{2}$AB=3$\sqrt {2}$，
∴CD=AD=3$\sqrt {2}$，选C．
点评：
本题主要考查了等腰直角三角形的性质，熟记性质是解题的关键．
一直角三角形的一条直角边长是7，另一条直角边与斜边长的和是49，则斜边的长（ ）
分析：
设另一直角边是x，斜边为(49-x)，根据勾股定理可求出解．
解答：
解：设另一直角边是x，
x+7_=(49-x)_
x=24，
49-24=25．
故斜边长是25．
故选D．
点评：
本题考勾股定理的应用，关键是设出另一个直角边为x，根据勾股定理可求出解．
在Rt△ABC中，∠C=90°，AB=15，AC：BC=3：4，则这个直角三角形的面积是（ ）
分析：
设AC=3x，则BC=4x，然后根据勾股定理得到AC_+BC_=AB_，求出x_的值，继而根据三角形的面积公式求出答案.
解答：
解：设AC=3x，则BC=4x，
根据勾股定理有AC_+BC_=AB_，
即(3x)_+(4x)_=15_，得：x_=9，
则△ABC的面积=
×3x×4x=6x_=54.
故选：C.
如图所示，四边形OABC为正方形，边长为6，点A，C分别在x轴，y轴的正半轴上，点D在OA上，且D的坐标为(2，0)，P是OB上的一动点，试求PD+PA和的最小值是( )
分析：
要求PD+PA和的最小值，PD，PA不能直接求，可考虑通过作辅助线转化PD，PA的值，从而找出其最小值求解．
解答：
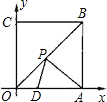
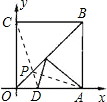解：连接CD，交OB于P．则CD就是PD+PA和的最小值．
∵在直角△OCD中，∠COD=90°，OD=2，OC=6，
∴CD=$\sqrt {}$=2$\sqrt {10}$，
∴PD+PA=PD+PC=CD=2$\sqrt {10}$．
∴PD+PA和的最小值是2$\sqrt {10}$．
故选A．
点评：
考查正方形的性质和轴对称及勾股定理等知识的综合应用．
如图所示，一个圆柱高为8cm，底面圆的半径为5cm，则从圆柱左下角A点出发．沿圆柱体表面到右上角B点的最短路程为( )
分析：
沿过A的圆柱的高AD剪开，展开得出平面，连接AB，根据勾股定理求出AB的长即可．
解答：
解：沿过A的圆柱的高AD剪开，展开得出平面，如图
连接AB，则AB的长就是从圆柱左下角A点出发．沿圆柱体表面到右上角B点的最短路程，
由题意知：∠BCA=90°，AC=$\frac {1}{2}$×2×5cm×π=5πcm，BC=8cm，
由勾股定理得：AB=$\sqrt {}$=$\sqrt {}$(cm)．
故选B．
点评：
本题考查了平面展开-最短路线问题，解此题的关键是知道求出哪一条线段的长，题目比较好，但是一道比较容易出错的题目．
如图，在底面周长为12，高为8的圆柱体上有A、B两点，则A、B两点的最短距离为( )
分析：
要求A、B两点间的最短距离，必须展开到一个平面内．只需展开圆柱的半个侧面，然后利用两点之间线段最短解答．
解答：
解：展开圆柱的半个侧面，得到一个矩形：矩形的长是圆柱底面周长的一半是6，矩形的宽是圆柱的高是8．再根据勾股定理求得矩形的对角线是10．
即A、B两点间的最短距离是10．
故选C．
点评：
要求不在同一个平面内的两点间的最短距离，必须把它们展开到一个平面内再进行计算．
如图Rt△ABC中，AB=BC=4，D为BC的中点，在AC边上存在一点E，连接ED，EB，则△BDE周长的最小值为( )
分析：
要求△BDE周长的最小值，就要求DE+BE的最小值．根据勾股定理即可得．
解答：
解：过点B作BO⊥AC于O，延长BO到B′，使OB′=OB，连接DB′，交AC于E，
此时DB′=DE+EB′=DE+BE的值最小．
连接CB′，易证CB′⊥BC，
根据勾股定理可得DB′=$\sqrt {}$=2$\sqrt {5}$，
则△BDE周长的最小值为2$\sqrt {5}$+2．
故选C．
点评：
此题考查了线路最短的问题，确定动点E何位置时，使DE+BE的值最小是关键．