单选题
一直角三角形的一条直角边长是7，另一条直角边与斜边长的和是49，则斜边的长（ ）
题目答案
D
您的答案
答案解析
分析：
设另一直角边是x，斜边为(49-x)，根据勾股定理可求出解．
解答：
解：设另一直角边是x，
x+7_=(49-x)_
x=24，
49-24=25．
故斜边长是25．
故选D．
点评：
本题考勾股定理的应用，关键是设出另一个直角边为x，根据勾股定理可求出解．
举一反三
在Rt△ABC中，∠C=90°，AB=15，AC：BC=3：4，则这个直角三角形的面积是（ ）
题目答案
C
您的答案
答案解析
分析：
设AC=3x，则BC=4x，然后根据勾股定理得到AC_+BC_=AB_，求出x_的值，继而根据三角形的面积公式求出答案.
解答：
解：设AC=3x，则BC=4x，
根据勾股定理有AC_+BC_=AB_，
即(3x)_+(4x)_=15_，得：x_=9，
则△ABC的面积=
×3x×4x=6x_=54.
故选：C.
如图所示，四边形OABC为正方形，边长为6，点A，C分别在x轴，y轴的正半轴上，点D在OA上，且D的坐标为(2，0)，P是OB上的一动点，试求PD+PA和的最小值是( )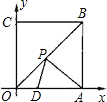
题目答案
A
您的答案
答案解析
分析：
要求PD+PA和的最小值，PD，PA不能直接求，可考虑通过作辅助线转化PD，PA的值，从而找出其最小值求解．
解答：
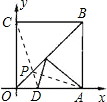解：连接CD，交OB于P．则CD就是PD+PA和的最小值．
∵在直角△OCD中，∠COD=90°，OD=2，OC=6，
∴CD=$\sqrt {}$=2$\sqrt {10}$，
∴PD+PA=PD+PC=CD=2$\sqrt {10}$．
∴PD+PA和的最小值是2$\sqrt {10}$．
故选A．
点评：
考查正方形的性质和轴对称及勾股定理等知识的综合应用．
如图所示，一个圆柱高为8cm，底面圆的半径为5cm，则从圆柱左下角A点出发．沿圆柱体表面到右上角B点的最短路程为( )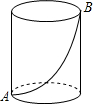
题目答案
B
您的答案
答案解析
分析：
沿过A的圆柱的高AD剪开，展开得出平面，连接AB，根据勾股定理求出AB的长即可．
解答：
解：沿过A的圆柱的高AD剪开，展开得出平面，如图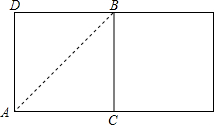
连接AB，则AB的长就是从圆柱左下角A点出发．沿圆柱体表面到右上角B点的最短路程，
由题意知：∠BCA=90°，AC=$\frac {1}{2}$×2×5cm×π=5πcm，BC=8cm，
由勾股定理得：AB=$\sqrt {}$=$\sqrt {}$(cm)．
故选B．
点评：
本题考查了平面展开-最短路线问题，解此题的关键是知道求出哪一条线段的长，题目比较好，但是一道比较容易出错的题目．
如图，在底面周长为12，高为8的圆柱体上有A、B两点，则A、B两点的最短距离为( )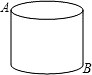
题目答案
C
您的答案
答案解析
分析：
要求A、B两点间的最短距离，必须展开到一个平面内．只需展开圆柱的半个侧面，然后利用两点之间线段最短解答．
解答：
解：展开圆柱的半个侧面，得到一个矩形：矩形的长是圆柱底面周长的一半是6，矩形的宽是圆柱的高是8．再根据勾股定理求得矩形的对角线是10．
即A、B两点间的最短距离是10．
故选C．
点评：
要求不在同一个平面内的两点间的最短距离，必须把它们展开到一个平面内再进行计算．
如图Rt△ABC中，AB=BC=4，D为BC的中点，在AC边上存在一点E，连接ED，EB，则△BDE周长的最小值为( )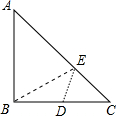
题目答案
C
您的答案
答案解析
分析：
要求△BDE周长的最小值，就要求DE+BE的最小值．根据勾股定理即可得．
解答：
解：过点B作BO⊥AC于O，延长BO到B′，使OB′=OB，连接DB′，交AC于E，
此时DB′=DE+EB′=DE+BE的值最小．
连接CB′，易证CB′⊥BC，
根据勾股定理可得DB′=$\sqrt {}$=2$\sqrt {5}$，
则△BDE周长的最小值为2$\sqrt {5}$+2．
故选C．
点评：
此题考查了线路最短的问题，确定动点E何位置时，使DE+BE的值最小是关键．
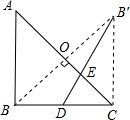
如图，在锐角△ABC中，AB=6，∠BAC=60°，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是( )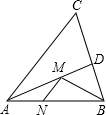
题目答案
B
您的答案
答案解析
分析：
在AC上取一点E，使得AE=AB，过E作EN⊥AB于N，交AD于M，连接BM，BE，BE交AD于O，根据两点之间线段最短和垂线段最短得出此时BM+MN最小，求出E和B关于AD对称，求出BM+MN′=EN′，求出EN′，即可求出答案．
解答：
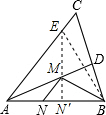解：在AC上取一点E，使得AE=AB，过E作EN⊥AB于N′，交AD于M，连接BM，BE，BE交AD于O，则BM+MN最小(根据两点之间线段最短；点到直线垂直距离最短)，
∵AD平分∠CAB，AE=AB，
∴EO=OB，AD⊥BE，
∴AD是BE的垂直平分线(三线合一)，
∴E和B关于直线AD对称，
∴EM=BM，
即BM+MN′=EM+MN′=EN′，
∵EN′⊥AB，
∴∠ENA=90°，
∵∠CAB=60°，
∴∠AEN′=30°，
∵AE=AB=6，
∴AN=$\frac {1}{2}$AE=3，
在△AEN中，由勾股定理得：EN=$\sqrt {}$=$\sqrt {}$=3$\sqrt {3}$，即BM+MN的最小值是3$\sqrt {3}$．
故选B．
点评：
本题考查的是轴对称-最短路线问题，涉及到垂线的性质，勾股定理，含30度角的直角三角形性质，轴对称的性质，等腰三角形的性质等知识点的综合运用．
如图，在锐角△ABC中，∠BAC=45°，AB=2，∠BAC的平分线交BC于点D，M、N分别是AD和AB上的动点，则BM+MN的最小值是( )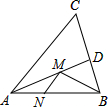
题目答案
C
您的答案
答案解析
分析：
作BH⊥AC，垂足为H，交AD于M′点，过M′点作M′N′⊥AB，垂足为N′，则BM′+M′N′为所求的最小值，再根据AD是∠BAC的平分线可知M′H=M′N′，再由锐角三角函数的定义即可得出结论．
解答：
解：如图，作BH⊥AC，垂足为H，交AD于M′点，过M′点作M′N′⊥AB，垂足为N′，则BM′+M′N′为所求的最小值．
∵AD是∠BAC的平分线，
∴M′H=M′N′，
∴BH是点B到直线AC的最短距离(垂线段最短)，
∵AB=4，∠BAC=45°，
∴BH=AB•sin45°=2×$\frac {$\sqrt {2}$}{2}$=$\sqrt {2}$．
∵BM+MN的最小值是BM′+M′N′=BM′+M′H=BH=$\sqrt {2}$．
故选C．
点评：
本题考查的是轴对称-最短路线问题，解答此类问题时要从已知条件结合图形认真思考，通过角平分线性质，垂线段最短，确定线段和的最小值．
如图，在锐角△ABC中，AB=6，∠BAC=45°，∠BAC的平分线交BC于点D，M，N分别是AD和AB上的动点，则BM+MN的最小值是( )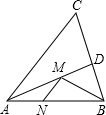
题目答案
C
您的答案
答案解析
分析：
作BH⊥AC，垂足为H，交AD于M′点，过M′点作M′N′⊥AB，垂足为N′，则BM′+M′N′为所求的最小值，再根据AD是∠BAC的平分线可知M′H=M′N′，再由锐角三角函数的定义即可得出结论．
解答：
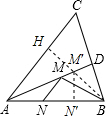
解：如图，作BH⊥AC，垂足为H，交AD于M′点，过M′点作M′N′⊥AB，垂足为N′，则BM′+M′N′为所求的最小值．
∵AD是∠BAC的平分线，
∴M′H=M′N′，
∴BH是点B到直线AC的最短距离(垂线段最短)，
∵AB=6，∠BAC=45°，
∴BH=AB•sin45°=6×$\frac {$\sqrt {2}$}{2}$=3$\sqrt {2}$．
∵BM+MN的最小值是BM′+M′N′=BM′+M′H=BH=3$\sqrt {2}$．
故选C．
点评：
本题考查的是轴对称-最短路线问题，解答此类问题时要从已知条件结合图形认真思考，通过角平分线性质，垂线段最短，确定线段和的最小值．
如图，在底面半径为2，(π取3)高为8的圆柱体上有只小虫子在A点，它想爬到B点，则爬行的最短路程是( )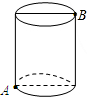
题目答案
A
您的答案
答案解析
分析：
A、B之间的最短路程为两直角边分别为圆柱的高，底面周长的一半的直角三角形的斜边长．
解答：
解：底面周长的一半为：2π≈6，
∴高等于8，
∴最短路程为：$\sqrt {}$=10，
故选：A．
点评：
此题主要考查了最短路径问题；立体几何中的最短路径问题，通常整理为平面几何中两点之间距离问题．
如图，已知等边△ABC的边长为6，点D为AC的中点，点E为BC的中点，点P为BD上一点，则PE+PC的最小值为( )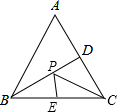
题目答案
D
您的答案
答案解析
分析：
由题意可知点A、点C关于BD对称，连接AE交BD于点P，由对称的性质可得，PA=PC，故PE+PC=AE，由两点之间线段最短可知，AE即为PE+PC的最小值．
解答：
解：∵△ABC是等边三角形，点D为AC的中点，点E为BC的中点，
∴BD⊥AC，EC=3，
连接AE，线段AE的长即为PE+PC最小值，
∵点E是边BC的中点，
∴AE⊥BC，
∴AE=$\sqrt {}$=$\sqrt {}$=3$\sqrt {3}$，
∴PE+PC的最小值是3$\sqrt {3}$．
故选D．
点评：
本题考查的是轴对称-最短路线问题，熟知等边三角形的性质是解答此题的关键．