分析:
由三角形ABC为等腰直角三角形,可得出AB=BC,∠ABC为直角,可得出∠ABD与∠EBC互余,在直角三角形ABD中,由两锐角互余,利用等角的余角相等得到一对角相等,再由一对直角相等,及AB=BC,利用AAS可得出三角形ABD与三角形BEC全等,根据全等三角形的对应边相等可得出BD=CE,由CE=3得出BD=3,在直角三角形ABD中,由AD=2,BD=3,利用勾股定理即可求出AB的长.
解答:
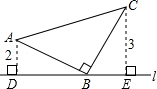 解:如图所示:
解:如图所示:
∵△ABC为等腰直角三角形,
∴AB=BC,∠ABC=90°,
∴∠ABD+∠CBE=90°,
又AD⊥BD,∴∠ADB=90°,
∴∠DAB+∠ABD=90°,
∴∠CBE=∠DAB,
在△ABD和△BCE中,
$\left\{\begin{matrix}∠ADB=∠BEC=90° \ ∠DAB=∠CBE \ AB=BC \ \end{matrix}\right.$,
∴△ABD≌△BCE,
∴BD=CE,又CE=3,
∴BD=3,
在Rt△ABD中,AD=2,BD=3,
根据勾股定理得:AB=$\sqrt {}$=$\sqrt {13}$.
故选D
点评:
此题考查了全等三角形的判定与性质,等腰直角三角形的性质,以及勾股定理,利用了转化的数学思想,灵活运用全等三角形的判定与性质是解本题的关键.
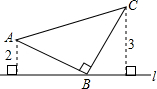
 解:如图所示:
解:如图所示: