如图,以点O为位似中心,将五边形ABCDE放大后得到五边形A′B′C′D′E′,已知OA=10cm,OA′=20cm,则五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比值是:.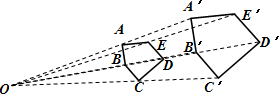
题目答案
您的答案
答案解析
分析:
由五边形ABCDE与五边形A′B′C′D′E′位似,可得五边形ABCDE∽五边形A′B′C′D′E′,又由OA=10cm,OA′=20cm,即可求得其相似比,根据相似多边形的周长的比等于其相似比,即可求得答案.
解答:
∵五边形ABCDE与五边形A′B′C′D′E′位似,OA=10cm,OA′=20cm,
∴五边形ABCDE∽五边形A′B′C′D′E′,且相似比为:OA:OA′=10:20=1:2,
∴五边形ABCDE的周长与五边形A′B′C′D′E′的周长的比为:OA:OA′=1:2.
故答案为:1:2.
点评:
此题考查了多边形位似的知识.注意位似是相似的特殊形式与相似多边形的周长的比等于其相似比知识的应用.
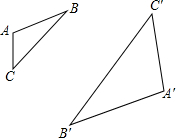
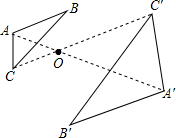 解:∵△ABC与△A′B′C′是位似图形
解:∵△ABC与△A′B′C′是位似图形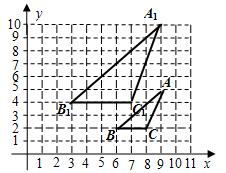

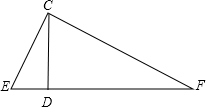 解:如图:过点C作CD⊥EF,
解:如图:过点C作CD⊥EF,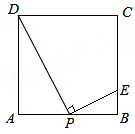
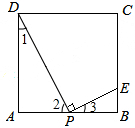 解:设AP=x,BE=y.
解:设AP=x,BE=y.