如图,△ABC为等边三角形,AB=6,动点O在△ABC的边上从点A出发沿着A→C→B→A的路线匀速运动一周,速度为1个长度单位每秒,以O为圆心、$\sqrt {}$为半径的圆在运动过程中与△ABC的边第二次相切时是出发后第秒.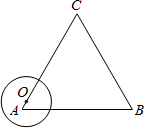
题目答案
您的答案
答案解析
分析:
若以O为圆心、$\sqrt {}$为半径的圆在运动过程中与△ABC的边第二次相切,即为当点O在AC上,且和BC边相切的情况.作O′D⊥BC于D,则O′D=$\sqrt {}$,利用解直角三角形的知识,进一步求得O′C=2,从而求得O′A的长,进一步求得运动时间.
解答:
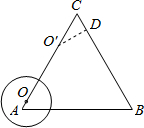 解:根据题意,则作O′D⊥BC于D,则O′D=$\sqrt {}$.
解:根据题意,则作O′D⊥BC于D,则O′D=$\sqrt {}$.
在Rt△O′CD中,∠C=60°,O′D=$\sqrt {}$,
∴O′C=2,
∴O′A=6-2=4,
∴以O为圆心、$\sqrt {}$为半径的圆在运动过程中与△ABC的边第二次相切时是出发后第4秒.
故答案为:4.
点评:
此题考查了直线和圆相切时数量之间的关系,能够正确分析出以O为圆心、$\sqrt {}$为半径的圆在运动过程中与△ABC的边第二次相切时的位置.
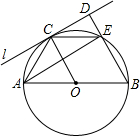

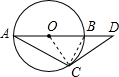 解:连接OC,BC,
解:连接OC,BC,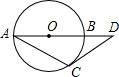
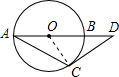 解:连接OC,
解:连接OC,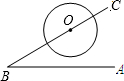
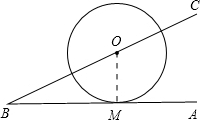 解:设切点为M,连接OM,
解:设切点为M,连接OM,