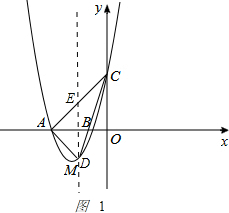
如图,已知抛物线y=ax+bx+3与x轴交于A、B两点,过点A的直线l与抛物线交于点C,其中A点的坐标是(1,0),C点坐标是(4,3).在抛物线的对称轴上是否存在点D,使△BCD的周长最小,则D的坐标为(,).
题目答案
您的答案
答案解析
分析:
利用待定系数法求二次函数解析式,利用待定系数法求出直线AC的解析式,然后根据轴对称确定最短路线问题,直线AC与对称轴的交点即为所求点D.
解答:
解:∵抛物线y=ax+bx+3经过点A(1,0),点C(4,3),
∴$\left\{\begin{matrix}a+b+3=0 \ 16a+4b+3=3 \ \end{matrix}\right.$,
解得$\left\{\begin{matrix}a=1 \ b=-4 \ \end{matrix}\right.$,
所以,抛物线的解析式为y=x-4x+3;
∵点A、B关于对称轴对称,
∴点D为AC与对称轴的交点时△BCD的周长最小,
设直线AC的解析式为y=kx+b(k≠0),
则$\left\{\begin{matrix}k+b=0 \ 4k+b=3 \ \end{matrix}\right.$,
解得$\left\{\begin{matrix}k=1 \ b=-1 \ \end{matrix}\right.$,
所以,直线AC的解析式为y=x-1,
∵y=x-4x+3=(x-2)_-1,
∴抛物线的对称轴为直线x=2,
当x=2时,y=2-1=1,
∴抛物线对称轴上存在点D(2,1),使△BCD的周长最小;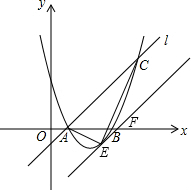
点评:
本题考查了二次函数综合题型,主要考查了待定系数法求二次函数解析式,待定系数法求一次函数解析式,利用轴对称确定最短路线问题,联立两函数解析式求交点坐标,利用平行线确定点到直线的最大距离问题.
 ,
,
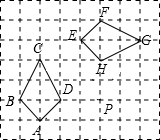
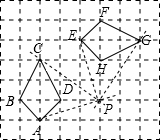 解:四边形ABCD旋转得到四边形EFGH时的旋转中心用有序数对表示是(5,2).
解:四边形ABCD旋转得到四边形EFGH时的旋转中心用有序数对表示是(5,2).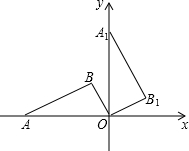
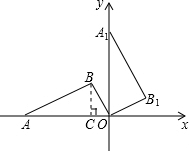
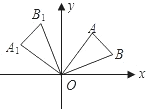
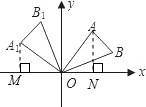 解:做A$_1$M⊥x轴于点M,AN⊥x轴于点N,易得△A$_1$MO≌△ONA,
解:做A$_1$M⊥x轴于点M,AN⊥x轴于点N,易得△A$_1$MO≌△ONA,