已知抛物线y=ax+bx+c的部分图象如图所示,若y>0,则x的取值范围是<x<.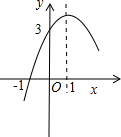
题目答案
您的答案
答案解析
分析:
由图可知,该函数的对称轴是x=1,则x轴上与-1对应的点是3.观察图象可知y>0时x的取值范围.
解答:
已知抛物线与x轴的一个交点是(-1,0)对称轴为x=1,
根据对称性,抛物线与x轴的另一交点为(3,0),
观察图象,当y>0时,-1<x<3.
点评:
此题的关键是根据二次函数的对称轴与对称性,找出抛物线y=ax+bx+c的完整图象.
已知抛物线y=ax+bx+c的部分图象如图所示,若y>0,则x的取值范围是<x<.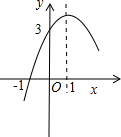
分析:
由图可知,该函数的对称轴是x=1,则x轴上与-1对应的点是3.观察图象可知y>0时x的取值范围.
解答:
已知抛物线与x轴的一个交点是(-1,0)对称轴为x=1,
根据对称性,抛物线与x轴的另一交点为(3,0),
观察图象,当y>0时,-1<x<3.
点评:
此题的关键是根据二次函数的对称轴与对称性,找出抛物线y=ax+bx+c的完整图象.
如图所示,抛物线y=ax+bx+c(a≠0)与x轴的两个交点分别为A(-1,0)和B(2,0),当y<0时,x的取值范围是x<或x>.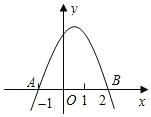
分析:
直接从图上可以分析:y<0时,图象在x轴的下方,共有2部分:一是A的左边,即x<-1;二是B的右边,即x>2.
解答:
观察图象可知,抛物线与x轴两交点为(-1,0),(2,0),
y<0,图象在x轴的下方,所以答案是x<-1或x>2.
点评:
考查了二次函数的图象与函数值之间的联系,函数图象所表现的位置与y值对应的关系,典型的数形结合题型.
已知二次函数y=ax+bx+c(a≠0)的图象如图所示,则一元二次不等式ax+bx+c>0的解是<x<.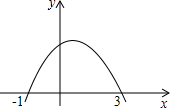
分析:
根据函数图象写出二次函数图象在x轴上方部分的x的取值范围即可.
解答:
解:由图可知,一元二次不等式ax+bx+c>0的解是-1<x<3.
故答案为:-1<x<3.
点评:
本题考查了二次函数与不等式,此类题目利用数形结合的思想求解更简便.
如图是抛物线y=ax+bx+c的图象,则由图象可知,不等式ax+bx+c<0的解集是<x<.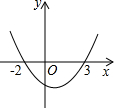
分析:
根据函数图象,写出x轴下方部分的函数图象x的取值范围即可.
解答:
解:由图可知,不等式ax+bx+c<0的解集是-2<x<3.
故答案为:-2<x<3.
点评:
本题考查了二次函数与不等式组,利用数形结合的思想是解题的关键.
如图,抛物线y=ax+bx+c交x轴于点A(-2,0)、B(3,0),则不等式ax+bx+c>0的解集是x>或x<.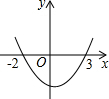
分析:
由函数图象可以得出当x=-2或x=3时,y的值为0,根据y=ax+bx+c,就可以结合图象得出ax+bx+c>0的解集.
解答:
解:由题意,得
x=-2或x=3时,y的值为0.
∵y=ax+bx+c,ax+bx+c>0,
∴x>3或x<-2时ax+bx+c>0.
故答案为:x>3或x<-2.
点评:
本题考查了二次函数的解析式的运用,二次函数与不等式的关系的运用,数形结合思想的运用,解答时分析函数的图象的数据关系是关键.
如图,小明的父亲在相距2米的两棵树间拴了一根绳子,给他做了一个简易的秋千,拴绳子的地方距地面高都是2.5米,绳子自然下垂呈抛物线状,身高1米的小明距较近的那棵树0.5米时,头部刚好接触到绳子,则绳子的最低点距地面的距离为米.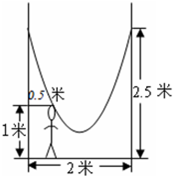
分析:
根据题意,运用待定系数法,建立适当的函数解析式,代入求值即可解答.
解答:
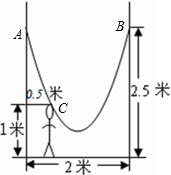 解:以左边树与地面交点为原点,地面水平线为x轴,左边树为y轴建立平面直角坐标系,
解:以左边树与地面交点为原点,地面水平线为x轴,左边树为y轴建立平面直角坐标系,
由题意可得A(0,2.5),B(2,2.5),C(0.5,1)
设函数解析式为y=ax+bx+c
把A、B、C三点分别代入得出c=2.5
同时可得4a+2b+c=2.5,0.25a+0.5b+c=1
解之得a=2,b=-4,c=2.5.
∴y=2x-4x+2.5=2(x-1)_+0.5.
∵2>0
∴当x=1时,y=0.5米.
∴故答案为:0.5米.
点评:
本题考查点的坐标的求法及二次函数的实际应用.此题为数学建模题,借助二次函数解决实际问题.
某种商品每件进价为20元,调查表明:在某段时间内若以每件x元(20≤x≤30,且x为整数)出售,可卖出(30-x)件.若使利润最大,每件的售价应为元.
分析:
本题是营销问题,基本等量关系:利润=每件利润×销售量,每件利润=每件售价-每件进价.再根据所列二次函数求最大值.
解答:
设最大利润为w元,
则w=(x-20)(30-x)=-(x-25)_+25,
∵20≤x≤30,
∴当x=25时,二次函数有最大值25,
故答案是:25.
点评:
本题考查了把实际问题转化为二次函数,再利用二次函数的性质进行实际应用.此题为数学建模题,借助二次函数解决实际问题.
某果园有100棵橘子树,平均每一棵树结600个橘子.根据经验估计,每多种一颗树,平均每棵树就会少结5个橘子.设果园增种x棵橘子树,果园橘子总个数为y个,则果园里增种棵橘子树,橘子总个数最多.
分析:
根据题意设多种x棵树,就可求出每棵树的产量,然后求出总产量y与x之间的关系式,进而求出x=-$\frac {b}{2a}$时,y最大.
解答:
解:假设果园增种x棵橘子树,那么果园共有(x+100)棵橘子树,
∵每多种一棵树,平均每棵树就会少结5个橘子,
∴这时平均每棵树就会少结5x个橘子,
则平均每棵树结(600-5x)个橘子.
∵果园橘子的总产量为y,
∴则y=(x+100)(600-5x)
=-5x+100x+60000,
∴当x=-$\frac {b}{2a}$=-$\frac {100}{2×(-5)}$=10(棵)时,橘子总个数最多.
故答案为:10.
点评:
此题主要考查了二次函数的应用,准确分析题意,列出y与x之间的二次函数关系式是解题关键.
出售某种手工艺品,若每个获利x元,一天可售出(8-x)个,则当x=元,一天出售该种手工艺品的总利润y最大.
分析:
先根据题意得出总利润y与x的函数关系式,再根据二次函数的最值问题进行解答.
解答:
解:∵出售某种手工艺品,若每个获利x元,一天可售出(8-x)个,
∴y=(8-x)x,即y=-x+8x,
∴当x=-$\frac {b}{2a}$=-$\frac {8}{-2}$=4时,y取得最大值.
故答案为:4.
点评:
本题考查的是二次函数的最值问题,能根据题意得出y与x的关系式是解答此题的关键.
某种火箭被竖直向上发射时,它的高度h(m)与时间t(s)的关系可以用公式h=-5t_+150t+10表示.经过s,火箭达到它的最高点.
分析:
由题意得:当火箭到达最高点时,即h达到最大值,本题可运用完全平方式求得最大值.
解答:
解:当火箭到达最高点时,即h达到最大值.
h=-5t_+150t+10
=-5(t-15)_+1135.
∵-5<0
∴t=15时,h取得最大值,即火箭达到最高点.
故应填15.
点评:
本题考查的是二次函数最大值的求法,这一题可用完全平方式求得.
某花圃用花盆培育某种花苗,经过试验发现每盆的盈利与每盆的株数构成一定的关系,每盆植入3株时,平均单株盈利3元,以同样的栽培条件,若每盆增加2株,平均单株盈利就减少0.5元,则每盆植株时能使单盆取得最大盈利;若需要单盆盈利不低于13元,则每盆需要植或株(按从小到大顺序填写答案).
分析:
根据已知假设每盆花苗(原来花盆中有3株)增加a(a为偶数)株,盈利为y元,则每盆花苗有(a+3)株,得出平均单株盈利为(3-0.5×$\frac {a}{2}$)元,由题意得y=(a+3)(3-0.5×$\frac {a}{2}$),根据二次函数的性质即可求得.
解答:
解:设每盆花苗(假设原来花盆中有3株)增加a(a为偶数)株,盈利为y元,
则根据题意得:y=(3-0.5×$\frac {a}{2}$)(a+3)
=-$\frac {1}{4}$(a-$\frac {9}{2}$)_+$\frac {63}{16}$,
∵a为偶数,
∴a=4,
∵当a=2时,y=7.5<13
当a=4时,y=(3-0.5×$\frac {4}{2}$)×(4+3)=14>13,
当a=6时,y=(3-0.5×$\frac {6}{2}$)×(6+3)=13.5>13,
∴每盆植7株时能使单盆取得最大盈利;若需要单盆盈利不低于13元,则每盆需要植7或9株.
故答案为7、7或9.
点评:
此题考查了二次函数的应用,根据每盆花苗株数×平均单株盈利=总盈利得出方程是解题关键.