如图,点E、F、G、H分别是任意四边形ABCD中AD、BD、BC、CA的中点,当四边形ABCD的边至少满足{_ _}条件时,四边形EFGH是菱形.
题目答案
您的答案
答案解析
分析:
首先利用三角形的中位线定理证出EF∥AB,EF=$\frac {1}{2}$AB,HG∥AB,HG=$\frac {1}{2}$AB,可得四边形EFGH是平行四边形,再根据邻边相等的平行四边形是菱形,添加条件AB=CD后,证明EF=EH即可.
解答:
解:需添加条件AB=CD.
∵E,F是AD,DB中点,
∴EF∥AB,EF=$\frac {1}{2}$AB,
∵H,G是AC,BC中点,
∴HG∥AB,HG=$\frac {1}{2}$AB,
∴EF∥HG,EF=HG,
∴四边形EFGH是平行四边形,
∵E,H是AD,AC中点,
∴EH=$\frac {1}{2}$CD,
∵AB=CD,
∴EF=EH,
∴四边形EFGH是菱形.
故答案为:A.
点评:
此题主要考查了三角形中位线定理与菱性的判定方法,菱形的判别方法是说明一个四边形为菱形的理论依据,常用三种方法:①定义;②四边相等;③对角线互相垂直平分.
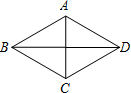
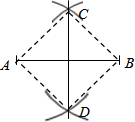
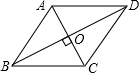

 解:邻边相等的平行四边形为菱形.如图,要使▱ABCD成为菱形,则需添加的一个条件是BA=BC.
解:邻边相等的平行四边形为菱形.如图,要使▱ABCD成为菱形,则需添加的一个条件是BA=BC.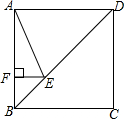
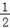 ,
,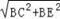 =
=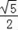 ,
,
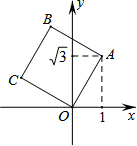
 解:如图,过点A作AD⊥x轴于D,过点C作CE⊥x轴于E,
解:如图,过点A作AD⊥x轴于D,过点C作CE⊥x轴于E,