分析：

根据切线长公式进行求解即可．

解答：

解：圆心坐标为O(0，0)，半径r=1，P(2，0)

则OP=2，

则切线长为$\sqrt {4−1}$=$\sqrt {3}$，

故答案为：$\sqrt {3}$，故选C．

点评：

本题主要考查直线和圆相切的性质，根据切弦长公式是解决本题的关键．比较基础．

分析：

根据双曲线方程，可得该双曲线的焦点在x轴上，由平方关系算出c=$\sqrt {}$=2，即可得到双曲线的焦点坐标．

解答：

解：∵双曲线方程为$\frac {x}{3}^{2}$-y²=1∴双曲线的焦点在x轴上，且a²=3，b²=1由此可得c=2，∴该双曲线的焦点坐标为(±2，0)故选：C

点评：

本题给出双曲线方程，求它的焦点坐标，着重考查了双曲线的标准方程和焦点坐标求法等知识，属于基础题．

分析：

由题意和商的关系化简所给的式子，求出tanα的值，利用倍角的正切公式求出tan2α的值．

解答：

解：由题意得，$\frac {sinα+cosα}{sinα-coα}$=2，

即$\frac {tanα+1}{tanα-1}$=2，解得tanα=3，

∴tan2α=$\frac {2tanα}{1-tan_α}$=-$\frac {3}{4}$，

故选A．

点评：

本题考查了利用商的关系化简齐次式，以及倍角的正切公式的应用．

分析：

根据等腰△ABC的腰为底的2倍，可先求出tan$\frac {A}{2}$，进而根据二倍角的正切公式可得答案．

解答：

解：依题意可得：tan$\frac {A}{2}$=$\frac {$\sqrt {15}$}{15}$，

故tanA=$\frac {2tan$\frac {A}{2}$}{1-tan_$\frac {A}{2}$}$=$\frac {2×$\frac {$\sqrt {15}$}{15}$}{1-($\frac {$\sqrt {15}$}{15}$)}$=$\frac {$\sqrt {15}$}{7}$，

故选D．

点评：

本题主要考查二倍角的正切公式．

分析：

由通项公式，令n=3即可得出．

解答：

解：令n=3，则a$_3$=(-1)_(3_+1)=-10．

故选A．

点评：

本题考查了利用数列的通项公式求值，属于基础题．

分析：

将“c_=(a-b)_+6”展开，另一方面，由余弦定理得到c_=a_+b_-2abcosC，比较两式，得到ab的值，计算其面积．

解答：

解：由题意得，c_=a_+b_-2ab+6，

又由余弦定理可知，c_=a_+b_-2abcosC=a_+b_-ab，

∴-2ab+6=-ab，即ab=6．

∴S_△ABC=$\frac {1}{2}$absinC=$\frac {3$\sqrt {3}$}{2}$．

故选：C．

点评：

本题是余弦定理的考查，在高中范围内，正弦定理和余弦定理是应用最为广泛，也是最方便的定理之一，高考中对这部分知识的考查一般不会太难，有时也会和三角函数，向量，不等式等放在一起综合考查．

分析：

利用复数的乘法法则即可得出．

解答：

解：原式=2-1+i+2i=1+3i．

故选：A．

点评：

本题考查了复数的乘法法则，属于基础题．

分析：

把直线的参数方程代入曲线的方程，利用参数的几何意义即可得出．

解答：

解：极坐标方程为ρ=6cosθ+6sinθ+$\frac {9}{ρ}$可化为ρ_=6ρcosθ+6ρsinθ+9，直角坐标方程为(x-3)_+(y-3)_=27．

直线的标准的参数方程为：$\left\{\begin{matrix}x=-1+$\frac {4}{5}$t \ y=-$\frac {3}{5}$t \ \end{matrix}\right.$(t为参数)

把直线的标准的参数方程代人圆方程得，t_-$\frac {14}{5}$t-2=0①

设t$_1$，t$_2$是方程①的两个实根，则t$_1$t$_2$=-2

∴|PA|•|PB|=|t$_1$||t$_2$|=|t$_1$t$_2$|=2．

故答案为：2．

点评：

熟练掌握极坐标方程与直角坐标方程的互化、直线参数方程的参数的几何意义是解题的关键．

分析：

直接利用等比数列的定义逐一判断给出的四个数列即可得到答案．

解答：

解：数列{a_n}是等比数列，设其公比为q，

①∵$\frac {a$_2$n+2}{a$_2$n}$=$\frac {a$_1$q}{a$_1$q}$=q_为常数，∴数列{a$_2$n}是等比数列；

②∵$\frac {a_n+1+a_n}{a_n+a_n-1}$=$\frac {q(a_n+a_n-1)}{a_n+a_n-1}$=q为常数，∴数列{a_n+a_n-1}是等比数列；

③若数列{a_n}是常数列，且各项为1，则数列{lga_n}不是等比数列；

④∵$\frac {|a_n+1|}{|a_n|}$=|$\frac {a_n+1}{a_n}$|=|q|为常数，∴数列{|a_n|}是等比数列．

∴给出的数列中仍是等比数列的有3个．

故选：C．

点评：

本题考查了等比数列的性质，考查了等比关系的确定，训练了学生思考问题的严谨性，是中档题．

分析：

根据焦点坐标得出a_-b_=50，将直线的方程与椭圆的方程组成方程组，消去y得到关于x的方程，再根据根与系数的关系求得AB的中点的横坐标的表达式，最后根据联立的方程求出其a，b即可求椭圆的方程．

解答：

解：设椭圆的标准方程为$\frac {x}{a}$+$\frac {y}{b}$=1(a＞b＞0)，

由F(0，5$\sqrt {2}$)，

∴c=5$\sqrt {2}$，

∴a_-b_=50．

把直线方程y=3x-2代入椭圆方程整理得(a_+9b_)x-12b_x+b_(4-a_)=0．

设弦的两个端点为A(x$_1$，y$_1$)，B(x$_2$，y$_2$)，

则由根与系数的关系得x$_1$+x$_2$=$\frac {12b}{a_+9b}$，

又AB的中点的横坐标为$\frac {1}{2}$，

∴$\frac {6b}{a_+9b}$=$\frac {1}{2}$，

∴a_=3b_，与方程a_-b_=50联立可解出a_=75，b_=25．

故椭圆的方程$\frac {x}{25}$+$\frac {y}{75}$=1．

故选C．

点评：

本题主要考查了椭圆的标准方程、直线与圆锥曲线的综合问题，考查韦达定理的运用，属于中档题．

分析：

先利用正弦定理化简已知等式，求出sinA的值，由A为锐角，利用特殊角的三角函数值即可求出A的度数；再由余弦定理列出关系式，再利用完全平方公式变形，将a，b+c及cosA的值代入求出bc的值，再由sinA的值，利用三角形面积公式即可求出三角形ABC的面积．

解答：

点评：

此题考查了正弦定理，三角形的面积公式，熟练掌握正弦定理是解本题的关键．

分析：

逐一分析各个选项中的对应是否满足映射的概念，即前一个集合中的每一个元素在后一个集合中是否都有唯一确定的元素和它对应．

解答：

解：如果一个集合中的任何元素在另一个集合中都有唯一确定的一个元素和它对应，则此对应构成映射．

故选项D构成映射，

对于选项A：集合B中4在集合A中对应两个数1，2，故此对应不是映射．

对于选项B：不能构成映射，因为前边的集合中的元素2，4在后一个集合中没有元素和它对应，故此对应不是映射．

对于选项C：集合B中5在集合A中对应两个数1，2，所以C是错误的．

故选D．

点评：

本题考查映射的概念，即一个集合中的任何元素在另一个集合中都有唯一确定的一个元素和它对应，则此对应构成映射．

分析：

化已知直线方程为斜截式，可得直线的斜率．

解答：

解：化已知直线方程为斜截式可得y=-$\frac {$\sqrt {3}$}{3}$x+$\sqrt {3}$，

可得直线的斜率为-$\frac {$\sqrt {3}$}{3}$，

故选C

点评：

本题考查直线的斜率，化直线的方程为斜截式是解决问题的关键，属基础题．

分析：

根据二项式的展开式的二项式系数是64，写出二项式系数的表示式，得到次数n的值，写出通项式，当x的指数是0时，得到结果．

解答：

解：∵$C_n^{0}+C_n^{1}+…+C_n^{n}$=2ⁿ=64，∴n=6．T$_{r+1}$=C$_6^{r}x^{6-r}{(\frac{1}{x})}^{r}$=，令6-2r=0，∴r=3，常数项：T$_4$=C$_6^{3}$=20，故选B．

点评：

本题是一个典型的二项式问题，主要考查二项式的性质，注意二项式系数和项的系数之间的关系，这是容易出错的地方，本题考查展开式的通项式，这是解题的关键．

分析：

首先，分两种情形进行讨论：ω＞0和ω＜0，然后，分别求解即可．

解答：

解：∵函数f(x)=2sinωx在区间[-$\frac {π}{3}$，$\frac {π}{4}$]上的最小值是-2，

∴当ω＞0时，$\frac {T}{4}$≥$\frac {π}{3}$，

∴ω≥$\frac {3}{2}$，

当ω＜0时，$\frac {T}{4}$≥$\frac {π}{4}$，

∴ω≤-2，

综上，符合条件的实数ω的取值范围为：(-∞，-2]∪[$\frac {3}{2}$，+∞)．

故答案为：(-∞，-2]∪[$\frac {3}{2}$，+∞)，选A．

点评：

本题重点考查了函数的单调性与周期性等知识，属于基础题．

分析：

本题考查线性回归直线方程，可根据回归直线方程一定经过样本中心点这一信息，选择验证法或排除法解决，具体方法就是将点(4，5)的坐标分别代入各个选项，满足的即为所求．

解答：

解：法一：

由回归直线的斜率的估计值为1.23，可排除D

由线性回归直线方程样本点的中心为(4，5)，

将x=4分别代入A、B、C，其值依次为8.92、9.92、5，排除A、B

法二：

因为回归直线方程一定过样本中心点，

将样本点的中心(4，5)分别代入各个选项，只有C满足，

故选C

点评：

本题提供的两种方法，其实原理都是一样的，都是运用了样本中心点的坐标满足回归直线方程．

分析：

利用二项式定理的展开式将二项式展开，利用组合数公式化简展开式，列出方程求出a，b，求出a+b．

解答：

解：

∵(1+$\sqrt {3}$)_=C$_4$($\sqrt {3}$)_+C$_4$($\sqrt {3}$)_+C$_4$($\sqrt {3}$)_+C$_4$($\sqrt {3}$)_+C$_4$($\sqrt {3}$)_=1+4$\sqrt {3}$+18+12$\sqrt {3}$+9=28+16$\sqrt {3}$由已知，得28+16$\sqrt {3}$=a+b$\sqrt {3}$，∴a+b=28+16=44．故选A．

点评：

本题考查二项式定理的展开式；要熟练掌握公式．

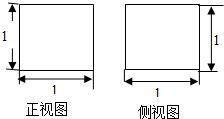
分析：

解法1：结合选项，正方体的体积否定A，推出正确选项C即可．

解法2：对四个选项A求出体积判断正误；B求出体积判断正误；C求出几何体的体积判断正误；同理判断D的正误即可．

解答：

解：解法1：由题意可知当俯视图是A时，即每个视图是边长为1的正方形，那么此几何体是立方体，显然体积是1，注意到题目体积是$\frac {1}{2}$，知其是立方体的一半，可知选C．

解法2：当俯视图是A时，正方体的体积是1；

当俯视图是B时，该几何体是圆柱，底面积是$\frac {π}{4}$S=π×($\frac {1}{2}$)_=$\frac {π}{4}$，高为1，则体积是$\frac {π}{4}$；

当俯视图是C时，该几何是直三棱柱，

故体积是V=$\frac {1}{2}$×1×1×1=$\frac {1}{2}$，

当俯视图是D时，该几何是圆柱切割而成，

其体积是V=$\frac {1}{4}$π×1_×1=$\frac {π}{4}$．

故选C．

点评：

本题是基础题，考查几何体的三视图的识别能力，作图能力，依据数据计算能力；注意三视图的投影规则是主视、俯视 长对正；主视、左视高平齐，左视、俯视 宽相等．

分析：

随机变量ξ服从二项分布，故可直接利用期望公式进行计算，求出p．

解答：

解：∵随机变量ξ服从二项分布ξ～B(9，p)，且Eξ=3，

∴Eξ=9p=3，

∴p=$\frac {1}{3}$．

故选：C．

点评：

本题主要考查二项分布的期望的简单应用，考查学生的计算能力，正确运用公式是关键．

分析：

写出①的逆命题，利用代入方程后，可判断A答案的真假；写出②的否命题，根据实数的性质，可以判断B的真假；判断③的真假，进而根据互为逆否的两个命题真假性相同，可以判断C答案的真假；写出④的逆命题，进而根据奇数和偶数的定义，可以判断D的真假，进而得到答案．

解答：

解：①若x-3x+2=0，则x=1或x=2的逆命题为：若x=1或x=2，则x-3x+2=0，为真命题，故A正确；

②若-2≤x＜3，则(x-2)(x-3)≤0的否命题为：若x＜-2或x≥3，则(x-2)(x-3)＞0，为假命题，故B错误；

③若x=y=0，则x+y_=0为真命题，故其逆否命题也为真，故C错误；

④若x、y∈N_，x+y是奇数，则x、y中一个是奇数，一个是偶数的逆命题为：若x、y中一个是奇数，一个是偶数，则x+y是奇数为真命题，故D错误．

故选A

点评：

本题考查的知识点是四种命题的真假关系，其中熟练掌握四种命题的定义，给出答案中原命题的逆命题，否命题，逆否命题是解答本题的关键．