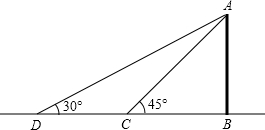
周末,身高都为1.6米的小芳、小丽来到溪江公园,准备用她们所学的知识测算南塔的高度.如图,小芳站在A处测得她看塔顶的仰角α为45°,小丽站在B处(A、B与塔的轴心共线)测得她看塔顶的仰角β为30°.她们又测出A、B两点的距离为30米.假设她们的
眼睛离头顶都为10cm,则可计算出塔高约为(结果精确到0.01,参考数据:$\sqrt {2}$≈1.414,$\sqrt {3}$≈1.732)( )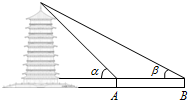
题目答案
您的答案
答案解析
分析:
由已知设塔高为x米,则由已知可得到如下关系,$\frac {x-1.6+0.1}{x-1.6+0.1+30}$=tan30°,从而求出塔高.
解答:
解:已知小芳站在A处测得她看塔顶的仰角α为45°,小丽站在B处(A、B与塔的轴心共线)测得她看塔顶的仰角β为30°,A、B两点的距离为30米.假设她们的眼睛离头顶都为10cm,
所以设塔高为x米则得:
$\frac {x-1.6+0.1}{x-1.6+0.1+30}$=tan30°=$\frac {$\sqrt {3}$}{3}$,
解得:x≈42.48,
即塔高约为42.48米.
故选:D.
点评:
此题考查的是解直角三角形的应用,关键是由已知得等腰直角三角形,根据直角三角函数列出方程求解.
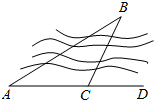
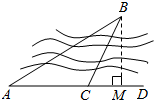 解:过B作BM⊥AD,
解:过B作BM⊥AD,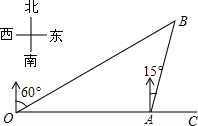
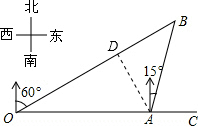 解:如图,过点A作AD⊥OB于D.
解:如图,过点A作AD⊥OB于D.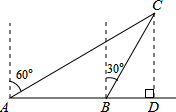

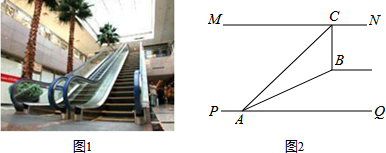
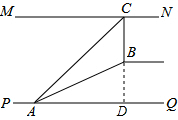 解:延长CB交PQ于点D.
解:延长CB交PQ于点D.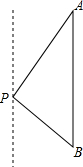
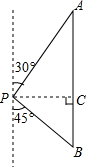 解:过点P作PC⊥AB于点C,
解:过点P作PC⊥AB于点C,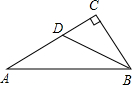
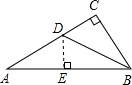 解:作DE⊥AB于点E.
解:作DE⊥AB于点E.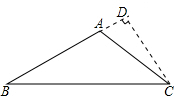 解:延长BA作CD⊥BD,
解:延长BA作CD⊥BD,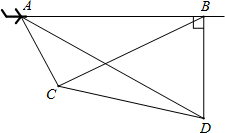 飞行了6千米到B处时,往后测得山头C的俯角为30°,而山头D恰好在飞机的正下方.山头C、D之间的距离为{_ _}千米.
飞行了6千米到B处时,往后测得山头C的俯角为30°,而山头D恰好在飞机的正下方.山头C、D之间的距离为{_ _}千米.