已知△ABC中,∠C=90°,tanA=$\frac {1}{2}$,D是AC上一点,∠CBD=∠A,则sin∠ABD=( )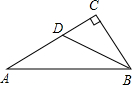
题目答案
您的答案
答案解析
分析:
作DE⊥AB于点E,根据相等的角的三角函数值相等即可得到$\frac {BC}{AC}$=$\frac {CD}{BC}$=$\frac {DE}{AE}$=$\frac {1}{2}$,设CD=1,则可以求得AD的长,然后利用勾股定理即可求得DE、AE的长,则BE可以求得,根据同角三角函数之间的关系即可求解.
解答:
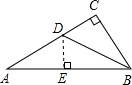 解:作DE⊥AB于点E.
解:作DE⊥AB于点E.
∵∠CBD=∠A,
∴tanA=tan∠CBD=$\frac {BC}{AC}$=$\frac {CD}{BC}$=$\frac {DE}{AE}$=$\frac {1}{2}$,
设CD=1,则BC=2,AC=4,
∴AD=AC-CD=3,
在直角△ABC中,AB=$\sqrt {}$=$\sqrt {4+16}$=2$\sqrt {5}$,
在直角△ADE中,设DE=x,则AE=2x,
∵AE_+DE_=AD_,
∴x+(2x)_=9,
解得:x=$\frac {3$\sqrt {5}$}{5}$,
则DE=$\frac {3$\sqrt {5}$}{5}$,AE=$\frac {6$\sqrt {5}$}{5}$.
∴BE=AB-AE=2$\sqrt {5}$-$\frac {6$\sqrt {5}$}{5}$=$\frac {4$\sqrt {5}$}{5}$,
∴tan∠DBA=$\frac {DE}{BE}$=$\frac {3}{4}$,
∴sin∠DBA=$\frac {3}{5}$.
故选A.
点评:
本题考查了三角函数的定义,以及勾股定理,正确理解三角函数就是直角三角形中边的比值是关键.
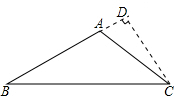 解:延长BA作CD⊥BD,
解:延长BA作CD⊥BD,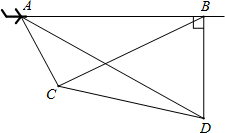 飞行了6千米到B处时,往后测得山头C的俯角为30°,而山头D恰好在飞机的正下方.山头C、D之间的距离为{_ _}千米.
飞行了6千米到B处时,往后测得山头C的俯角为30°,而山头D恰好在飞机的正下方.山头C、D之间的距离为{_ _}千米.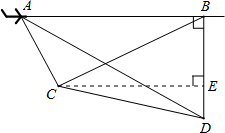
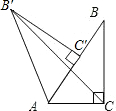
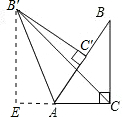 解:如图,作B′E⊥AC交CA的延长线于E.
解:如图,作B′E⊥AC交CA的延长线于E.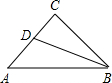
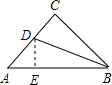 解:作DE⊥AB于E点.
解:作DE⊥AB于E点.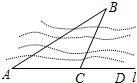
 解:过点B作BE⊥AD于E.
解:过点B作BE⊥AD于E.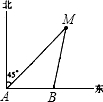
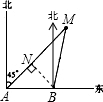 解:如图,过点B作BN⊥AM于点N.
解:如图,过点B作BN⊥AM于点N.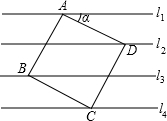
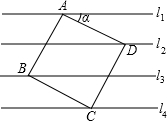
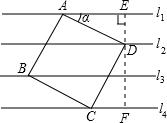 解:过D作EF⊥l$_1$,交l$_1$于E,交l$_4$于F,
解:过D作EF⊥l$_1$,交l$_1$于E,交l$_4$于F,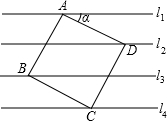
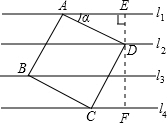
 解:如图,过点D作DE⊥l$_1$于点E并反向延长交l$_4$于点F,
解:如图,过点D作DE⊥l$_1$于点E并反向延长交l$_4$于点F,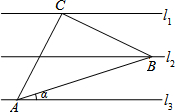
 解:如图,过点A作AD⊥l$_1$于D,过点B作BE⊥l$_1$于E,设l$_1$,l$_2$,l$_3$间的距离为1,
解:如图,过点A作AD⊥l$_1$于D,过点B作BE⊥l$_1$于E,设l$_1$,l$_2$,l$_3$间的距离为1,