在一次夏令营活动中,小霞同学从营地A点出发,要到距离A点1000m的C地去,先沿北偏东70°方向到达B地,然后再沿北偏西20°方向走了500m到达目的地C,此时小霞在营地A的( )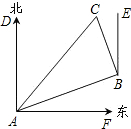
题目答案
您的答案
答案解析
分析:
根据方位角的概念及已知转向的角度结合三角函数的知识求解.
解答:
 解:A点沿北偏东70°的方向走到B,则∠BAD=70°,
解:A点沿北偏东70°的方向走到B,则∠BAD=70°,
B点沿北偏西20°的方向走到C,则∠EBC=20°,
又∵∠BAF=90°-∠DAB=90°-70°=20°,
∴∠1=90°-20°=70°,
∴∠ABC=180°-∠1-∠CBE=180°-70°-20°=90°.
∵AC=1000m,BC=500m,
∴sin∠CAB=500÷1000=$\frac {1}{2}$,
∴∠CAB=30°,
∴∠DAC=∠BAD-∠CAB=40°.
故小霞在营地A的北偏东40°方向上.
故选C.
点评:
解答此类题需要从运动的角度,再结合三角函数的知识求解.本题求出∠ABC=90°是解题的关键.
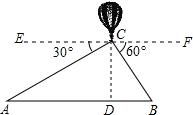
 解:如图.由题意可知,AB=5km,∠2=30°,∠EAB=60°,∠3=30°.
解:如图.由题意可知,AB=5km,∠2=30°,∠EAB=60°,∠3=30°.
 解:过点A作AC⊥x轴于C.
解:过点A作AC⊥x轴于C.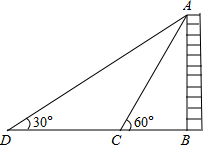
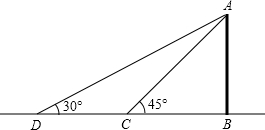
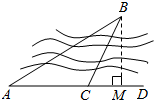 解:过B作BM⊥AD,
解:过B作BM⊥AD,
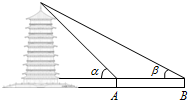
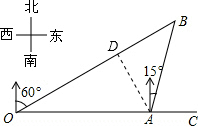 解:如图,过点A作AD⊥OB于D.
解:如图,过点A作AD⊥OB于D.