如图,在坐标平面上,Rt△ABC为直角三角形,∠ABC=90°,AB垂直x轴,M为Rt△ABC的外心.若A点坐标为(3,4),M点坐标为(-1,1),则B点坐标为何( )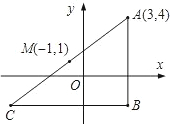
题目答案
您的答案
答案解析
分析:
本题可先根据坐标系中线段中点的计算方法解出C点的坐标,再根据AB垂直x轴,BC平行y轴即可得出B点的坐标.
解答:
 解:如图:
解:如图:
作MN∥BC,
∵∠ABC=90°,AB垂直x轴,M为Rt△ABC的外心,
∴AM=CM,AM:CM=AN:BN,MN∥x轴.
∵若A点坐标为(3,4),M点坐标为(-1,1),
∴N点的坐标为(3,1),
∴B点的坐标为(3,-2),
故选B.
点评:
此题考查了外心的性质、直角三角形的性质及平行线的性质,解题的关键是充分运用数形结合的思想从而解决问题.

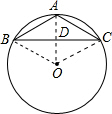 解:连接OA交BC于点D,连接OC,OB,
解:连接OA交BC于点D,连接OC,OB,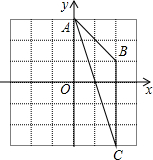
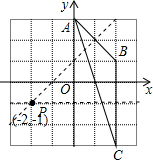 解:作AB与BC的垂直平分线,它们相交于点P(-2,-1).
解:作AB与BC的垂直平分线,它们相交于点P(-2,-1).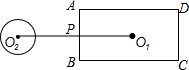
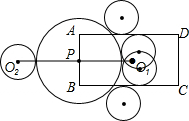 解:如图,⊙O$_2$与矩形的边只有一个公共点的情况一共出现4次,
解:如图,⊙O$_2$与矩形的边只有一个公共点的情况一共出现4次,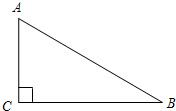
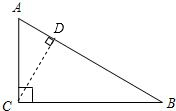 解:作CD⊥AB于点D.
解:作CD⊥AB于点D.